Páginas de Ernesto de Jesús Alcañiz UNIVERSIDADDE ALCALÁ Departamento de Química Inorgánica

<< Anterior               Índice               Siguiente >>

Ampliaciones de Enlace Químico y Estructura de la Materia (1º Químicas)

=====>Disponible en formato PDF

Resolución de la ecuación de Schrödinger para el átomo de hidrógeno

En un átomo de hidrógeno, o en general en un átomo o ion con un sólo electrón, el electrón se mueve en un campo esférico y centrado en el núcleo cuyo potencial es:

(1)

donde Z es el número atómico (para el hidrógeno, Z = 1) y r es la distancia entre el núcleo y el electrón. La ecuación de Schrödinger para un átomo monoelectrónico queda de la siguiente manera:

(2)

NOTA: Utilizamos la masa del electrón m_e aunque debería utilizarse de forma más precisa su masa reducida.

La ecuación (2) se resuelve de forma más simple si se utilizan coordenadas polares en lugar de cartesianas porque el potencial depende únicamente de la coordenada r en el sistema polar pero de las tres coordenadas x, y, z en un sistema cartesiano. En tal caso se puede demostrar que las soluciones se pueden descomponer en un producto de tres funciones más simples, cada una de las cuales sólo depende de una coordenada polar:

(3)

donde R recibe el nombre de función radial y y son las funciones angulares.

Sustitución de coordenadas cartesinas por polares

La relación entre las coordenadas polares y cartesianas es:

de donde se deduce que (la deducción no es evidente, por lo que no se desarrolla. Puede encontrarse por ejemplo en I. N. Levine, Química cuántica, editorial AC):

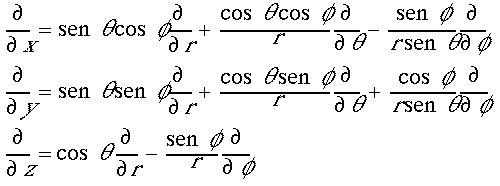
Elevando al cuadrado cada uno de los operadores anteriores y sumando, obtenemos el operador en coordenadas polares esféricas:

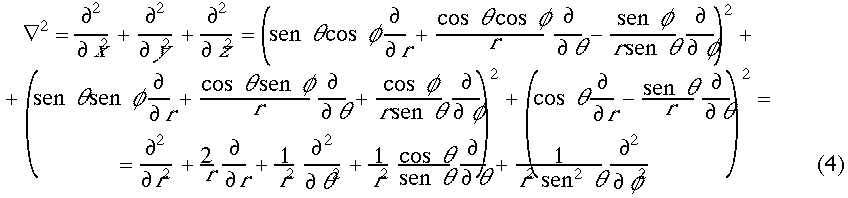
En la expresión (4), se pueden agrupar términos escribiéndola de la siguiente forma:

(5)

Tras sustituir (5) en (2), obtenemos la ecuación de Schrödinger en coordenadas polares (6), la cual parece mucho más complicada, pero de hecho es más fácil de resolver, tal como apuntaremos a continuación.

(6)

Sustitución de por R

Sustituyendo por el producto (3):

(7)

NOTA: Cambiamos la notación de derivadas parciales por la de totales ya que ahora cada derivada actúa sobre una función de una sóla coordenada.

Separación de las variables

Para resolver la ecuación hay que separar las variables, en nuestro caso r, y, en términos distintos. Multiplicando la ecuación (7) por (r²sen²)/(R) y reordenando términos:

(8)

En esta expresión, la variable está separada del resto en el tercer término. Cuando cambia , la suma del primer, segundo y cuarto términos no cambia, ya que en ninguno de ellos interviene , por lo que el tercer término tiene que ser constante también para que la suma pueda ser, para cualquer valor de , igual a cero. Por conveniencia, a esta constante le llamaremos -m_l²:

(9)

Podemos seguir separando variables. Sustituyendo (9) en (8) y dividiendo por sen²:

(10)

Obsérvese que el primer y cuarto términos dependen sólo de r, y el segundo y tercero de . Siguiendo el mismo razonamiento que hemos hecho para , la suma de los términos que dependen de r debe ser igual a una constante a la que, por conveniencia, llamaremos l(l + 1), y la suma de los términos que sólo dependen de debe ser igual a - l(l + 1). En resumen:

(11)

(12)

Resolución de la ecuación

Una solución a la ecuación (9) es

(13)

La constante a es la constante de normalización, es decir la necesaria para que se cunpla:

Por tanto su valor debe ser:

y la función queda como

(14)

Cualquiera que sea el valor de m_l, la función (14) es solución de la ecuación de Schrödinger. Ahora bien, las condiciones frontera que hemos impuesto a la función de onda para que su cuadrado pueda tener sentido físico, limitan los valores posibles para m_l. Una de dichas condiciones es que la función de onda tiene que tener un único valor en cada punto del espacio. Eso implica que el valor de para un ángulo tiene que ser igual que su valor para un ángulo 360deg. mayor (+ 2). En los siguentes ejemplos se muestra que esto sólo se cumple si m_l es un número entero (0, +/-1, +/-2, +/-3, etc):

ml	= a sen(ml)		= a sen(ml(+ 2))
0	a sen(0)	=	a sen(0)
+1	a sen()	=	a sen(+ 2)
+2	a sen(2)	=	a sen(2+ 4)
+1/2	a sen(/2)	distinto de	a sen(/2 +)

Hay una solución de por cada valor entero de m_l.

Resolución de las ecuaciones R y

La resolución de estas ecuaciones sigue etapas similares a las empleadas para . Sin embargo, al ser su resolución más compleja no será abordada y sólo señalaremos las conclusiones más importantes.

De la ecuación (8), es fácil deducir que en las funciones aparecen la constante m_l elevada al cuadrado (por lo que la función no depende del signo de m_l sino únicamente de su modulo|m_l|) y la constante l, cuyos valores están limitados a números enteros positivos por las condiciones frontera. Otra restricción importante es que l >= |m_l|.

Hay una solución de por cada valor entero y positivo de l y por cada valor de |m_l| menor o igual a l

Finalmente se resuelve la ecuación (7) en la que aparece una nueva constante n, de forma que en la función R aparecen esta contante y también la constante l_. Los valores de n están igualmente cuantizados por las condiciones frontera, solo pudiendo tomar valores enteros iguales o mayores de 1 y teniéndose además que cumplir que n>=l

Normalmente las dos funciones angulares se consideran conjuntamente, de forma que la parte angular de la función de onda toma la forma

A_l,ml(, ) = _l,|ml|() _ml()

Como _n,l,ml(r, , ) = R_n,l(r) _l,|ml|() _ml()

Hay una solución completa de por cada trío de valores de n, l y m_l donde n puede tomar cualquier valor entero igual o mayor de 1, l cualquier valor entero entre 0 y n -1, y m_l cualquier valor entero desde +l hasta -l